Math2.org Math Tables: Table of Integrals

Power of x.

xn dx = xn+1 (n+1)-1 + C (n 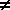 -1)  Proof

x-1 dx = ln|x| + C

Exponential / Logarithmic

ex dx = ex + C Proof	bx dx = bx / ln(b) + C Proof, Tip!
ln(x) dx = x ln(x) - x + C Proof

Trigonometric

sin x dx = -cos x + C Proof	csc x dx = - ln|csc x + cot x| + C Proof
cos x dx = sin x + C Proof	sec x dx = ln|sec x + tan x| + C Proof
tan x dx = -ln|cos x| + C Proof	cot x dx = ln|sin x| + C Proof

Trigonometric Result

cos x dx = sin x + C Proof	csc x cot x dx = - csc x + C Proof
sin x dx = -cos x + C Proof	sec x tan x dx = sec x + C Proof
sec2 x dx = tan x + C Proof	csc2 x dx = - cot x + C Proof

Inverse Trigonometric

arcsin x dx = x arcsin x + (1-x2) + C

arccsc x dx = x arccos x - (1-x2) + C

arctan x dx = x arctan x - (1/2) ln(1+x2) + C

Inverse Trigonometric Result
 

dx (1 - x2)  = arcsin x + C     dx  x (x2 - 1)  = arcsec|x| + C     dx  1 + x2  = arctan x + C

Useful Identities arccos x = /2 - arcsin x  (-1 <= x <= 1)  arccsc x = /2 - arcsec x  (|x| >= 1)  arccot x = /2 - arctan x  (for all x)

Hyperbolic

sinh x dx = cosh x + C Proof	csch x dx = ln |tanh(x/2)| + C Proof
cosh x dx = sinh x + C Proof	sech x dx = arctan (sinh x) + C
tanh x dx = ln (cosh x) + C Proof	coth x dx = ln |sinh x| + C Proof

---

Click on Proof for a proof/discussion of a theorem.

 

To solve a more complicated integral, see The Integrator at http://integrals.com.