I. Product Calculus

C. Definite Continuous Products

Deriving the Continuous Product

The definite continuous product (CP) is the second building block of product calculus to be investigated. It is defined in the preface as being the discrete product made continuous, and it can be expressed in terms of the discrete product.

We question how to make the discrete product continuous:
 x
f(k) = f(a) f(a+1) f(a+2) ... f(x)
k=a

To do so, we must change k's discrete range (a, a+1, a+2, .., x) into a continuous range [a, x). This can be expressed as:

lim  n-->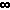

xn-1  f(k/n) = f(a) f(a+1/n) f(a + 2/n) ... f(x - 1/n)  k=an

An infinite product of finite functions such as this simply does not converge. The increased number of terms must compensated for in order to make the expansion converge.

The integral accomplishes this by multipling each term by the difference in successive k-values:

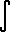f(t) dt =

lim  n-->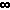

xn-1 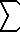 f(k/n) =  k=an

lim[ f(a) (1/n) + f(a+1/n) (1/n) + f(a + 2/n) (1/n) + .. + f(x) (1/n) ]

On preforming the same opperation with our expression, the product becomes:

lim  n-->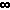

xn-1  [ f(k/n) (1/n) ] = 0  k=an

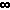
This will always converge to zero since as n-->, each f(k/n)(1/n) term approaches 0 (assuming f(k/n) is finite). This opperation is inadeguate for the continuous product.

We must find what opperation opp( ) reduces each term so that product both converges AND still resembles the discrete product. Let's try setting f(k) = c (a constant). It can be hypothysized that when f(k) is constant, both the discrete and continuous iterations of this type are equivalent. Note:

x-1
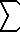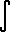
c =  c dx
k=a
(We set the upper summation limit to x-1 in order that its range is inclusive on the left but exclusive on the right.)

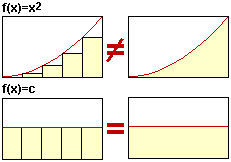
so we hypothysize:

x-1  f(k) =  k=a

lim  n-->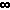

xn-1  opp [ f(k/n) ] = 0  k=an

for some opperation opp( ), when f(k)=c.

Such a blatent analogy is acceptable since the intent is to derive rather than prove the CP discrete expression. After all, we are working from abstract definitions of a calculs' building blocks. In the following sections we will see why such a constraint works.

Now, let a=1 and x=2 and expand both sides:

f(1) = lim (n-->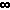) opp[f(1)] opp[f(1+1/n)] opp[f(1+2/n)] ... opp[f(2-1/n)]

Substitute f(k)=c:

c = lim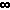 (n-->) opp(c) ⁿ
c^1/n = opp(c)  We now have our reducing opperation.

Placing the opp(c) = c^1/n into our CP expression:
 

lim  n-->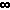

xn-1  f(k/n)1/n  k=an

We create a simplied notation with the symbol  to denote a product over a continuous range. Our new expression can be written:
 

x   f(t) dt =   a

lim   (n-->)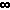

xn-1     k=an

f(k/n)1/n

Note that the k was replaced with t to indicate it is no longer constrainted to integer values. In the CP, f(t) is raised to the infinitisemal dt, instead of multiplied by it as with the integral. This is apparent because dt is the infinitisemal form of the 1/n counterpart.

Frequently, the CP will be shown expanded in the form:
b 
f(t) ^dt = f(a)^dt f(a+dt)^dt f(a+2dt)^dt ... f(b)^dt
_a
and it will be assumed that all dt terms approach infintity at the same rate.

Geometric Interpretation of the CP

The CP is equal to the product of the areas of each partition under the curve, raised to the width of the partition, when all the partitions are of infinitesimal size.

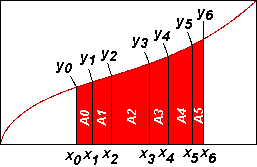
We divide the curve into partitions within an interval.  Therefore, by the definition above, the CP for this curve, under the interval x₀ < x < x₆, is APPROXIMATELY:
 
 

x6  f(t) dt ~=  x0

y0 (x1 - x0) y1 (x2-x1) y2 (x3-x2) y3 (x4-x3) y4 (x5-x4) y5(x6-x5)

The true CP is achieved when we select partitions with widths approaching zero, as our discrete iterative definition of the CP indicates:
 
 

x   f(t) dt =   a

lim   (n-->)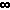

xn-1     k=an

f(k/n)1/n

 

Indefinite CP

The definite CP's we have been dealting with require a lower and upper bound. We will now explore a CP more basic than these, the indefinite CP.

The following identity readily stems from the CP's discrete iteration:

x  f(t) dt =  a

b  f(t) dt  a

x  f(t) dt  b

for arbitrary constant b.

Specifically, if a and b are constants, and we allow x to varry, then the left CP, being defined over the constant interval (a,b), never varies (it is a constant). In essence, we may write:

x  f(t) dt = c  a

x  f(t) dt  b

This equation enables us to standardize the lower bonds of CP's and only need to deal with the upper bound. This becomes useful in the next section when we compute the inverse opperation of the CP. We set the lower bound to a certain constant s on indefinite CP's. Why was this standard lower-bound chosen? We will see in the next section exactly why this definition is so convienient; for now, we will accept it as true.

When the CP is standardized, we may use the simplied, indefinite notation:

x
f(t) ^dt = f(t) ^dt.
s

To standardize a CP with a non-stanardized lower bound, we use the equations above:
 

x  f(t) dt =  a

s  f(t) dt  a

x  f(t) dt = c  s

x  f(t) dt  s

= c f(t) dt

 

when c =

s  f(t) dt  a

When tabulating CP's of functions, only the indefinite form will be expressed since it is simplified. Here is a sample table of CP's:

Table of CP's

a dt = ax

ex dt = e(x^2 / 2)

a(x^n) dt = a (x^(n+1)/(n+1))

 
Now suppose we know want to find:
2
e^{x dt} = e^{(x^2 / 2)}
1
using the CP table above.
 

The following identity is helpful:

x  f(t) dt =  a

x  f(t) dt  c

/

a  f(t) dt  c

It is easily derivable from the CP's iterative definition.

f(c)dx f(c+dx)dx f(c+2dx)dx ... f(x-dx) f(x)  f(c)dx f(c+dx)dx f(c+2dx)dx ... f(a-dx) f(a)

Most of the terms cancel out, leaving (a..x) f(t)^dx as the remainder.

By setting c=f ^-1(1), the identity can be rewritten in the following indefinite form:

x  f(t) dt =  a

x  f(t) dt

/

a  f(t) dt

since both unknown constants of the indefinite CP quotient cancel.

We now have the tools to solve our example porblem:

2  ax dt =  1

2  ax dt

/

1  ax dt

= e^{((2)^2 / 2)} / e^{((1)^2 / 2)} = e^3/2 = ~ 4.482

The answer can be checked by manually performing the equivalent iteration:

2 ex dt =   1

lim   (n-->)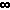

(2)n-1     k=(1)n

[e(k/n)]1/n

=~ 4.482

As we discover additional identites for CP's, we need only express them in indefinite form since they are readily convertable to their definite counterparts.

CP's of Functions

Continuous Product Identities

 

Identity	Description
c dt = cx
a(x^n) dt = a (x^(n+1)/(n+1))

 
 

Identity	Description
f(t)c dt = cx f(t)dt	Constant Rule  (special case of  the product rule)
f(t)g(t) dt = f(t)dt g(t)dt	Product Rule
f(t)/g(t) dt = f(t)dt / g(t)dt	Quotient Rule

 

If one so desires, a CP can be expressed in terms of a the following linear calculus integral expression and evaluated by linear calculus means.
 

b  f(x) dx = exp(  a

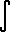ln f(x) dx )

This is similar to the relation:
 

b  f(k) = exp(  k=a

b 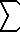 ln f(k) )  k=a

exp(x) is an equivalent notation for e^x

Derivation of the former relation:

b  f(x) dx =   a

lim _(dx-->0) f(a)^dx f(a+dx)^dx f(a+2dx)^dx ... f(b)^dx
= lim exp(ln( f(a)^dx f(a+dx)^dx f(a+2dx)^dx ... f(b)^dx ))
= lim exp( ( ln f(a) + ln f(a+dx) + ln f(a+2dx) + .. + ln f(b) ) dx )
= exp( 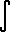 ln f(x) dx ).    Q.E.D.
The later relation can be derived by similar methods.
In the next section we will examine the anti-product, which is the third building block of product calculus examined and the inverse of the CP.

>>> Next Section <<< | Table of Contents