Math2.org Math Tables:
|
| (Math) |
| An Introduction to
Generalized Calculus |
Unit I - Product Calculus |
| Section D - Anti-Product |
| opp( | x
|
The CP is indefinite, so we may rewrite it:
x
![]() f(t)
dt
f(t)
dt
s
for an unknown lower-bound s. Expand the CP by it's iterative
definition:
x
![]() f(t)
dt = f(x)dt f(x-dt)dt f(x-2dt)dt
... f(s) = g(x)
f(t)
dt = f(x)dt f(x-dt)dt f(x-2dt)dt
... f(s) = g(x)
s
and define this as a function g(x)
A special result occurs when we try dividing g(x)/g(x-dt):
| g(x)/g(x-dt) = | f(x)dt f(x-dt)dt f(x-2dt)dt ... f(s)
f(x-dt)dt f(x-2dt)dt ... f(s) |
All the terms except f(x)dt cancel out, leaving:
g(x)/g(x-dt) = f(x)dt
rearranged as:
f(x) = [ g(x)/g(x-dt) ]1/dt
In simplied terms, this is denoted:
| qg(x) 1/dt = [ g(x)/g(x-dt) ]1/dt. |
This is our inverse function of the continuous product, named the anti-product.
The quantity g(x)/g(x-d) may be represented as the quotiential qg
which means the quotient of infinitely close terms. qg is an infinitesimal,
different than the differential dt, in that is is infinitely close to 1,
as opposed to infinitely close to 0.
Geometric Interpretation of the Anti-Product
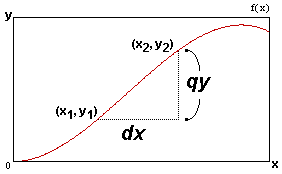
We define a new infinitesimal, qy, which instead of being infinitely
close to zero as in dx, is infinitly close to one. Note, qy is not the
length of the vertical increment of the curve over a dx--that is dy--it
is instead the quotient of both endpoints of the increment. These concepts
are clarified by the definition:
Now we can define the product calculus' counterpart of the derivative:
Definition of the Anti-Product:
The anti-product of f(x) at a point x=c is the limit of the quotient
in the y-values of two infinitismaly close points on the curve, centered
around the point x=c, raised to the reciprical of the difference in x-values
of the two points.
The above can be expressed:
qf(x) 1/dx = lim [ f(x2)/f(x1) ] 1/(x2-x1).
(or more simply...)
| qf(x) 1/dx = lim (d-->0) [ f(x+d)/f(x) ] 1/d. |
Consider the function f(x) = x2. We will compute its anti-product
at x=2 by inputing successively smaller values of d in the above
defintion.
| dx = x2 - x1 | qy = y2 / y1 | qy 1/dx |
| 1 | = 32/22
= 2.25 |
2.25 |
| 0.1 | = 2.12/22
= 1.1025 |
2.65330 |
| 0.01 | 1.010025 | 2.71152 |
| 0.001 | 1.00100025 | 2.71760 |
1 / 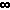 |
--- | 2.71828...
= e |
q(x2) 1/dx | (x=2) = e.
We can derive algebraically with our elementary theory of limits that
| q(xn) 1/dx = en/x. |
Table of Anti-Products
We can derive the following AP's (anti-products) and use them for our
convienence:
| f(x) | |
| xn | en/x |
| ax | a |
| ln(x) | e 1/(x ln x) |
| sin(x) | e cot(x) |
| cos(x) | e -tan(x) |
| tan(x) | e 1/(cos x sin x) |
| qf(x) 1/dx = e |
The following identities for AP's can be derived by a number of methods:
| Formula | Description |
| q(c f(x))1/dx = qf(x) 1/dx | Constant Rule |
| q(f(x)+g(x))1/dx = (q(ef)1/dx q(eg)1/dx)1/(f+g)
= (e df/dx e dg/dx)1/(f+g) |
Addition Rule |
| q(f(x)g(x)) 1/dx = qf(x) 1/dx qg(x) 1/dx | Product Rule |
| q(f(x)g(x))1/dx = f(x) |
Power Rule |
| qg(f(x)) 1/dx = (qg 1/df) df/dx | Chain Rule |
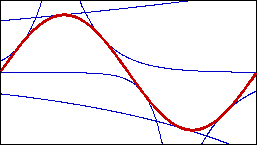
(product curve tangents on a sine wave)
The identity function of a calculus is the function whose continuous
limit is a constant. The identity function of the product calculus is the
one which satisfies the constraint:
The function ![]()
![]() (a + bx) =
(a + bx) = ![]() (bx) and q(abx) 1/dx = q(bx) 1/dx.
The constant b equals the value of the anti-iteration:
(bx) and q(abx) 1/dx = q(bx) 1/dx.
The constant b equals the value of the anti-iteration: ![]()
Since we have the form of the identity curve, we can fit a tangent identity curve on a function at given points, as shown in the above graph.
Graph of Tangent Product Curve on f(x) at x=c:
g(x) = b(x-c) f(c). where p=the qf(x)1/dx at
the point x=c.
The tangent curve may seem trivial--fitting a curve with the same AP on a function--but later on we will fit curves with similar successively higher AP's--2nd, 2rd, 4th, etc. AP--until the fitted curve equals the origional curve. That will essentially lead us to the product calculus equivalent of Taylor's Theorem, and from there will lead us to a generalized Taylor's Theorem for all calculus's.
An Example
Consider the function y = x! It can be represented in product notation
as:
x
![]() k = x!
k = x!
k=1
Euler's Gamma Function is the continuous equivalent of the factorial.
![]() (x+1) =
x!
(x+1) =
x!
Now we will derive a continuous approximation function for these two
functions.
Looking at the discrete product, we can see that with each increase
in x, the height of the curve is multiplied by its new x-value.
Therefore, we can estimate q(x!)1/dx at x to be approximately
x. To be more exact, we will say q(x!)1/dx at x
is approximately c+1/2. Knowing the AP of our approximation function, we
can get the origional function by taking the AP's CP (Fundamental Theorem
for Product Calculus). Note the similar appearance of the CP and the Discrete
Product.
x
![]() (t +
1/2) dt = exp(
(t +
1/2) dt = exp( ![]()
![]() ln(t + 1/2) dt )
ln(t + 1/2) dt )
1
(CP --> integral conversion)
| = exp( [ x ln(x) - x ] | x+1/2
x+1/2) |
) |
Our approximation formula is:
| x! = |
| x | x! = |
Approx. Formula |
| 1/2 | 0.886 | 0.897 |
| 1 | 1 | 1 |
| 2 | 2 | 1.979 |
| 3 | 6 | 5.909 |
| 4 | 24 | 23.574 |
| 5 | 120 | 117.674 |
| 150 | 5.713x10 262 | 5.562x10 262 |
Next, we advance to connect the Discrete Product, Continuous Product and Anti-Product into one cohesive theorem.