Math2.org Math Tables: Special Functions
|
| (Math) |
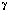constant = 0.5772156649...
![[Gamma]](/math//symbols/gamma-u.gif "[Gamma]")
(x) = ![[integral]](/math//symbols/integral.gif "[integral]")
tx-1 e-t dt
(Gamma function)
B(x,y) = 
tx-1 (1-t)y-1dt (Beta function)
Ei(x) = 
e-t/t dt (exponential integral) or it's variant, NONEQUIVALENT form:
Ei(x) =li(x) =(e^t - 1)/t dt = gamma + ln(x) +
(n=1..inf)x^n/(n*n!)
1/ln(t) dt (logarithmic integral)sin(t)/t dt (sine integral) or it's variant, NONEQUIVALENT form:Si(x) =
cos(t)/t dt (cosine integral) or it's variant, NONEQUIVALENT form:Ci(x) = -
(cosh(t)-1)/t dt (hyperbolic cosine integral)sinh(t)/t dt (hyperbolic sine integral)
![\[ Erf(x) = 2 \pi<sup>{2}</sup> \int_0^x exp(-t^2) \, dt \]](/math/tex/43061d5ec95a2f8dae93055b4c808eb2.png "\[ Erf(x) = 2 \pi<sup>{2}</sup> \int_0^x exp(-t^2) \, dt \]")
![\[ = 2 \pi<sup>{2}</sup> \sum_0^\infty (-1)^n x<sup>2n+1</sup> n!<sup>-1</sup> (2n+1)<sup>-1</sup> \]](/math/tex/5015d2d521064c3602852f941c4f5bb1.png "\[ = 2 \pi<sup>{2}</sup> \sum_0^\infty (-1)^n x<sup>2n+1</sup> n!<sup>-1</sup> (2n+1)<sup>-1</sup> \]")
(error function)
![\[ FresnelC(x) = \int_0^x \cos(\frac{1}{2}\pi t^2) \, dt \]](/math/tex/2377112893c95de9292031d841e6069f.png "\[ FresnelC(x) = \int_0^x \cos(\frac{1}{2}\pi t^2) \, dt \]")
![\[ FresnelS(x) = \int_0^x \sin(\frac{1}{2}\pi t^2) \, dt \]](/math/tex/b0a0d2339b9ab7390809054c7f0b40c5.png "\[ FresnelS(x) = \int_0^x \sin(\frac{1}{2}\pi t^2) \, dt \]")
dilog(x) = 
ln(t) (1-t)-1 dt
![\[ Psi(x) = \frac{d}{dx} ln(\Gamma(x)) \]](/math/tex/1d6ffbf4c01c45e0397af05b5cdb9300.png "\[ Psi(x) = \frac{d}{dx} ln(\Gamma(x)) \]")
Psi(n,x) = nth derivative of Psi(x)
W(x) = inverse of x ex
![\[ L_n(x) = \frac{1}{n!} e^x (x^n e<sup>-x</sup>)<sup>(n)</sup> \]](/math/tex/f59d53fcf5af7e8396ec7d66a49f1e49.png "\[ L_n(x) = \frac{1}{n!} e^x (x^n e<sup>-x</sup>)<sup>(n)</sup> \]")
(laguerre polynomial degree n. (n) meaning nth derivative)
![\[ Zeta(s) = \sum<sub>n=1</sub><sup>\infty</sup> n<sup>-s</sup> \]](/math/tex/f7fe77ab22fcb23b32d0945d0567727b.png "\[ Zeta(s) = \sum<sub>n=1</sub><sup>\infty</sup> n<sup>-s</sup> \]")
Dirichlet's beta function
![\[ B(x) = \sum<sub>n=0</sub>^\infty (-1)^n (2n+1)<sup>-x</sup> \]](/math/tex/dab6a73c25f8a3fa28d558ae6a9e564c.png "\[ B(x) = \sum<sub>n=0</sub>^\infty (-1)^n (2n+1)<sup>-x</sup> \]")
