Power Summations #2

Summation	Expansion	Equivalent Value	Comments
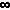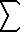1/n n=1	= 1 + 1/2 + 1/3 + 1/4 + ...	diverges to	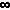see the gamma constant
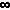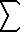1/n ² n=1	= 1 + 1/4 + 1/9 + 1/16 + ...	= (1/6) PI ² = 1.64493406684822...	see Expanisions of PI
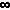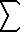1/n ³ n=1	= 1 + 1/8 + 1/27 + 1/81 + ...	= 1.20205690315031...	see the Unproved Theorems
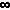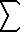1/n ⁴ n=1	= 1 + 1/16 + 1/81 + 1/256 + ...	= (1/90) PI ⁴ = 1.08232323371113...	see Expanisions of PI
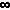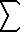1/n ⁵ n=1	= 1 + 1/32 + 1/243 + 1/1024 + ...	= 1.03692775514333...	see the Unproved Theorems
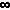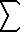1/n ⁶ n=1	= 1 + 1/64 + 1/729 + 1/4096 + ...	= (1/945) PI ⁶ = 1.017343061984449...	see Expanisions of PI
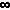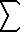1/n ⁷ n=1	= 1 + 1/128 + 1/2187 + 1/16384 + ...	= 1.00834927738192...	see the Unproved Theorems
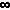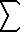1/n ⁸ n=1	= 1 + 1/256 + 1/6561 + 1/65536 + ...	= (1/9450) PI ⁸ = 1.00407735619794...	see Expanisions of PI
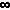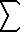1/n ⁹ n=1	= 1 + 1/512 + 1/19683 + 1/262144 + ...	= 1.00200839282608...	see the Unproved Theorems
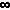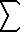1/n ¹⁰ n=1	= 1 + 1/1024 + 1/59049 + 1/1048576 + ...	= (1/93555) PI ¹⁰ = 1.00099457512781...	see Expanisions of PI
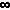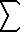1/n ^2k n=1	= 1 + 1/2 ^2k + 1/3 ^2k + 1/4 ^2k + ...	= (-1)^k-1 ( 2 ^2k B_(2k) PI^2k ) / ( 2(2k)! )	k is a positive integer. B_k are Bernoulli numbers. see Expanisions of PI

Math2.org Math Tables: Power Summations #2