Math2.org Math Tables:
|
| (Math) |
|
Sine and Cosine
Topics |
Sine and Cosine: Overview
The sine (abbreviated "sin") and cosine ("cos") are the two most prominent trigonometric functions. All other trig functions can be expressed in terms of them. In fact, the sine and cosine functions are closely related and can be expressed in terms of each other. Definition 1 is the simplest and most intuitive definition of the sine and cosine function. The sine definition basically says that, on a right triangle, the following measurements are related:
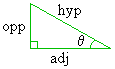

Futhermore, Definition I gives exact equations that describe each of these relations:
sin(q) = opposite / hypotenuse
cos(q) = adjacent / hypotenuse
This first equation says that if we evaluate the sine of that angle q, we will get the exact same value as if we divided the length of the side opposite to that angle by the length of the triangle's hypotenuse. This second equation says that if we evaluate the cosine of that angle q, we will get the exact same value as if we divided the length of the side adjacent to that angle by the length of the triangle's hypotenuse. These relations holds for any right triangle, regardless of size. The main result is this: If we know the values of any two of the above quantities, we can use the above relation to mathematically derive the third quantity. For example, the sine function allows us to answer any of the following three questions: "Given a right triangle, where the measurement of one of the non-right angles (q) is known and the length of the side opposite to that angle q is known, find the length of the triangle's hypotenuse." "Given a right triangle, where the measurement of one of the non-right angles (q) is known and the length of the triangle's hypotenuse is known, find the length of the side opposite to that angle q." "Given a right triangle, where the length of the triangle's hypotenuse and the length of one of the triangle's other sides is known, find the measurement of the angle (q) opposite to that other side."The cosine is similar, except that the adjacent side is used instead of the opposite side. The functions takes the forms y = sin(q) and x = cos(q). Usually, q is an angle measurement and x and y denotes lengths. The sine and cosine functions, like all trig functions, evaluate differently depending on the units on q, such as degrees, radians, or grads. For example, sin(90°) = 1, while sin(90)=0.89399.... explaination
Both functions are trigonometric cofunctions of each other,
in that function of the complementary angle, which is the "cofunction,"
is equal to the other function:
|