Math2.org Math Tables:

Since there are three sides and two non-right angles in a right triangle, the trigonometric functions will need a way of specifying which sides are related to which angle. (It is not-so-useful to know that the ratio of the lengths of two sides equals 2 if we do not know which of the three sides we are talking about. Likewise, if we determine that one of the angles is 40°, it would be nice to know of which angle this statement is true.

We need a way of labeling the sides. Consider a general right triangle:

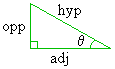
A right triangle has two non-right angles, and we choose one of these angles to be our angle of interest, which we label "q." ("q" is the Greek letter "theta.")

We can then uniquely label the three sides of the right triangle relative to our choice of q. As the above picture illustrates, our choice of q affects how the three sides get labeled.

We label the three sides in this manner: The side opposite the right angle is called the hypotenuse. This side is labeled the same regardless of our choice of q. The labeling of the remaining two sides depend on our choice of theta; we therefore speak of these other two sides as being adjacent to the angle q or opposite to the angle q. The remaining side that touches the angle q is considered to be the side adjacent to q, and the remaining side that is far away from the angle q is considered to be opposite to the angle q, as shown in the picture.