Math2.org Math Tables: Trigonometric Identities
|
| (Math) |
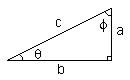
| sin(theta) = a / c | csc(theta) = 1 / sin(theta) = c / a |
| cos(theta) = b / c | sec(theta) = 1 / cos(theta) = c / b |
| tan(theta) = sin(theta) / cos(theta) = a / b | cot(theta) = 1/ tan(theta) = b / a |
| sin2(x) + cos2(x) = 1 | tan2(x) + 1 = sec2(x) | cot2(x) + 1 = csc2(x) | |
sin(x 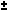 y) = sin x cos y y) = sin x cos y
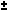 cos x sin
y cos x sin
y | |||
cos(x 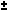 y) = cos x cosy y) = cos x cosy 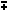 sin x sin
y sin x sin
y | |||
tan(x 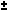 y) = (tan x
y) = (tan x 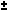 tan y) / (1
tan y) / (1 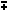 tan x tan y)
tan x tan y)
sin(2x) = 2 sin x cos x
cos(2x) = cos2(x) - sin2(x) = 2 cos2(x) - 1 = 1 - 2 sin2(x)
tan(2x) = 2 tan(x) / (1 - tan2(x))
sin2(x) = 1/2 - 1/2 cos(2x)
cos2(x) = 1/2 + 1/2 cos(2x)
sin x - sin y = 2 sin( (x - y)/2 ) cos( (x + y)/2 )
cos x - cos y = -2 sin( (x-y)/2 ) sin( (x + y)/2 )
| angle | 0 | 30 | 45 | 60 | 90 |
|---|---|---|---|---|---|
| sin2(a) | 0/4 | 1/4 | 2/4 | 3/4 | 4/4 |
| cos2(a) | 4/4 | 3/4 | 2/4 | 1/4 | 0/4 |
| tan2(a) | 0/4 | 1/3 | 2/2 | 3/1 | 4/0 |
a/sin(A) = b/sin(B) = c/sin(C) (Law of Sines)
| (Law of Cosines) |
(a - b)/(a + b) = tan 1/2(A-B) / tan 1/2(A+B) (Law of Tangents)
