An Introduction to
Generalized Calculus |
Unit I - Product Calculus |
| A. Introduction |
I. Product Calculus
A. Introduction
We will examine our first non-elementary calculus, the product calculus.
The product calculus is defined by a whole new set of building blocks.
It gets its name from the product expansion,

,
which we will refer to as the
discrete product for classification
reasons. Unlike the summation,
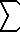
,
which is the sum of all terms, the

is the product of all its terms.
One may propose that we replace the 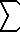 in the discrete iteration block with the
in the discrete iteration block with the  and build a new calculus from there:
and build a new calculus from there:
| Product Calculus |
Continuous |
Discrete |
| Limit |
? |
|
| Iteration |
? |

discrete product |
The other building blocks must be redefined in order to satisfy the conditions
mentioned in the preface:
-
The continuous iteration is discrete iteration made continuous.
-
The continuous limit and continuous iteration are inverses of each other.
The existence of the other two building blocks is hinted by the following
analogy:
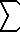 is
to
is
to  as
as 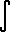 is to ?
is to ?
Furthermore, we may ask:
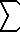 is to
is to 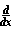 as
as  is to ?
is to ?
In the following sections, we will find out exactly what these building
blocks are:
| Product Calculus |
Continuous |
Discrete |
| Limit |
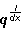
antiproduct |
|
| Iteration |

continuous product |

discrete product |
And from there precipitates a whole new calculus with its own rules and
theorems. Yet, it maintains key relationships with elementary calculus.
![]() in the discrete iteration block with the
in the discrete iteration block with the ![]() and build a new calculus from there:
and build a new calculus from there:
![]() is
to
is
to ![]() as
as ![]() is to ?
is to ?
![]() is to
is to ![]() as
as ![]() is to ?
is to ?