The Compound Interest Equation
P = C (1 + r/n) nt
where
P = future value
C = initial deposit
r = interest rate (expressed as a fraction: eg. 0.06)
n = # of times per year interest in compounded
t = number of years invested
Simplified Compound Interest Equation
When interest is only compounded once per yer (n=1), the equation simplifies to:
P = C (1 + r) t
Continuous Compound Interest
When interest is compounded continually (i.e. n -->
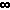
), the compound interest equation takes the form:
P = C e rt
Demonstration of Various Compounding
The following table shows the final principal (P), after t = 1 year and t = 10 years, of an account initally with C = $10000, at 6% interest rate, with the given compounding (n). As is shown, the method of compounding (n) has an effect that is initially small but becomes more significant over time (t).
| n | P (t=1) | P (t=10) |
| 1 (yearly) | $ 10600.00 | 17908.48 |
| 2 (semi-anually) | $ 10609.00 | 18061.11 |
| 4 (quarterly) | $ 10613.64 | 18140.18 |
| 12 (monthly) | $ 10616.78 | 18193.97 |
| 52 (weekly) | $ 10618.00 | 18214.89 |
| 365 (daily) | $ 10618.31 | 18220.27 |
| continuous | $ 10618.37 | 18221.19 |
Loan Balance
Situation: A person initially borrows an amount
A and
in return agrees to make
n repayments per year,
each of an amount
P.
While the person is repaying the loan, interest is accumulating
at an annual percentage rate of
r, and this interest
is compounded
n times a year (along with each payment). Therefore, the person
must continue paying these installments of amount
P until
the original amount and any accumulated interest is repayed.
This equation gives the amount
B that the person still
needs to repay after
t years.
|
B = A (1 + r/n)nt - P
|
(1 + r/n)nt - 1
(1 + r/n) - 1
|
where
B = balance after t years
A = amount borrowed
n = number of payments per year
P = amount paid per payment
r = annual percentage rate (APR)

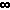 ), the compound interest equation takes the form:
), the compound interest equation takes the form:
