Math2.org Math Tables: Series Properties
|
| (Math) |
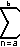 an is the indicated sum
of all values of an when n is set to each integer from a to b inclusive; namely, the indicated sum of the values aa + aa+1 + aa+2 + ... + ab-1 + ab.
an is the indicated sum
of all values of an when n is set to each integer from a to b inclusive; namely, the indicated sum of the values aa + aa+1 + aa+2 + ... + ab-1 + ab.
Definition of the "Sum of the Series":
The "sum of the series" is the actual result when all the terms of the series are summed.
Note the difference: "1 + 2 + 3" is an example of a "series," but "6" is the actual "sum of the series."
Algebraic Definition:
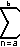 an = aa + aa+1 + aa+2 + ... + ab-1 + ab
an = aa + aa+1 + aa+2 + ... + ab-1 + ab
Summation Arithmetic:
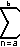 c an = c
c an = c 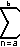 an (constant c)
an (constant c)
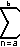 an +
an + 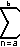 bn =
bn = 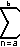 an + bn
an + bn
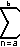 an -
an - 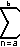 bn =
bn = 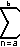 an - bn
an - bn
Summation Identities on the Bounds:
b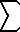 an ann=a |
c + 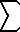 an ann=b+1 | c = 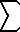 an ann = a |
| | (similar relations exist for subtraction and division as generalized below for any operation g) | |
b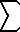 an ann=a |
g(b) = 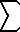 ag -1(c) ag -1(c)n=g(a) |
