Math2.org Math Tables: Chain Rule
|
| (Math) |
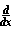 f(g(x)) = f(g(x)) = 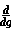 f(g) * f(g) * 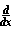 g(x) g(x)
|
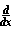 f(g(x)) =
f(g(x)) = 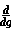 f(g) *
f(g) * 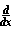 g(x)
from the definition
g(x)
from the definition
We can use the definition of the derivative:
Therefore,
f(x) =
lim
d-->0f(x+d)-f(x)
d
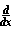 f(g(x)) can be written as such:
f(g(x)) can be written as such:
f(g(x)) = df/dx = (f(g(x+d) - f(g(x))/d
df/dx * 1/(dg/dx) = [ (f(g(x+d) - f(g(x))/d ] * [ d/(g(x+d) - g(x)) ]
= ( f(g(x+d))-f(g(x)) )/(g(x+d)-g(x)) = df/dg
df/dx = df/dg * dg/dx