Math2.org Math Tables: Conic Sections

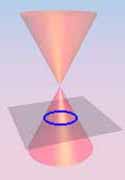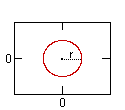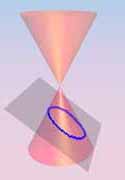
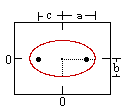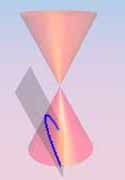
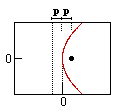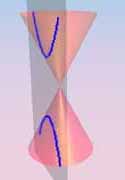
Circle	Ellipse (h)	Parabola (h)	Hyperbola (h)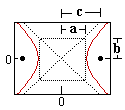
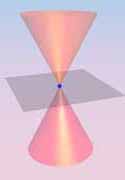
Definition: A conic section is the intersection of a plane and a cone.	Ellipse (v)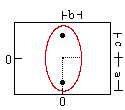	Parabola (v)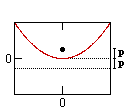	Hyperbola (v)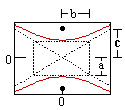

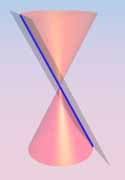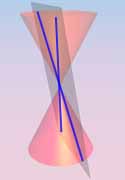By changing the angle and location of intersection, we can produce a circle, ellipse, parabola or hyperbola; or in the special case when the plane touches the vertex: a point, line or 2 intersecting lines.

Point	Line	Double Line

The General Equation for a Conic Section: Ax2 + Bxy + Cy2 + Dx + Ey + F = 0

The type of section can be found from the sign of: B² - 4AC

If B2 - 4AC is...	then the curve is a...
< 0	ellipse, circle, point or no curve.
= 0	parabola, 2 parallel lines, 1 line or no curve.
> 0	hyperbola or 2 intersecting lines.

The Conic Sections. For any of the below with a center (j, k) instead of (0, 0), replace each x term with (x-j) and each y term with (y-k).

	Circle	Ellipse	Parabola	Hyperbola
Equation (horiz. vertex):	x2 + y2 = r2	x2 / a2 + y2 / b2 = 1	4px = y2	x2 / a2 - y2 / b2 = 1
Equations of Asymptotes:				y = ± (b/a)x
Equation (vert. vertex):	x2 + y2 = r2	y2 / a2 + x2 / b2 = 1	4py = x2	y2 / a2 - x2 / b2 = 1
Equations of Asymptotes:				x = ± (b/a)y
Variables:	r = circle radius	a = major radius (= 1/2 length major axis) b = minor radius (= 1/2 length minor axis) c = distance center to focus	p = distance from vertex to focus (or directrix)	a = 1/2 length major axis b = 1/2 length minor axis c = distance center to focus
Eccentricity:	0		c/a	c/a
Relation to Focus:	p = 0	a2 - b2 = c2	p = p	a2 + b2 = c2
Definition: is the locus of all points which meet the condition...	distance to the origin is constant	sum of distances to each focus is constant	distance to focus = distance to directrix	difference between distances to each foci is constant
Related Topics:	Geometry section on Circles